The three utilities problem

1 Mar 2022

Here’s a puzzle known as the “three utilities problem”:

1. On a sheet of paper, draw a row of three points. These represent the “houses.”
2. Draw another row of three points to represent the “utilities.”
3. Draw a line from each house to each utility. (There should be nine lines in total.) The lines can be straight or curved, but must not intersect.

In the example below, the house on the top left is connected to all three utilities. To solve the puzzle, you need to do this with the other two houses such that none of the lines cross each other. Sounds easy, right?

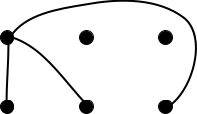
Unfortunately, this version of the puzzle is impossible. You can’t connect each house to each utility without some of the lines crossing. But the puzzle is solvable if you add an additional rule: the lines can go off any edge of paper and reappear on the opposite side. In mathematical language, the complete bipartite graph K_{3 3} cannot be embedded in the plane, but it can be embedded in the torus. (The two 3s refer to the fact that there are three houses and three utilities. A torus is a rectangle where you can go off the edge and “loop around” to the other side.) In the example below, the utility on the top left is connected to the house on the bottom right via a line that goes off the top of the page.

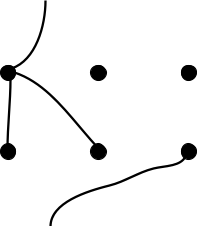
(Note that the horizontal position of the line stays the same when it reappears. Likewise, if a line goes off the left or right edge of the page, its vertical position must stay the same.)

Here are a few puzzles you can try:

1. Solve the three utilities problem on a torus. See if you can find a solution where only two lines go off the edge of the paper.
2. Add another house, so there are four houses and three utilities. See if you can find a solution where only four lines go off the edge.
3. Solve the problem with five houses and three utilities.
4. Solve the problem with four houses and four utilities.

Here are the solutions I found. The graphs are color-coded so that the lines connected to each utility are all the same color. This makes it easy to verify that the solutions are correct; you just need to check that each house is connected to one line of each color.

One can play a similar game with complete graphs instead of complete bipartite graphs.

1. Draw five points on a sheet of paper.
2. Draw a bunch of lines so that each point is connected directly to every other point. (There should be 10 lines in total.)
3. The lines are not allowed to intersect each other, but can go off any edge of the paper and loop around to the other side.
4. To make the puzzle harder, try the same thing with six points or seven points (it is impossible with eight).

Here are my solutions.